“貌似简单，会的寥寥无几！”这是一道小学五年级数学题：三角形仅一边已知，咋求面积？ 如图，点E在长方形ABCD边AB上，连接DE与CE，延长CE与DA、相交于点F，BE=8，AF=3，求阴影三角形ADE的面积。 有人说，简单，“瞪眼”便知阴影面积为12。 有人说，对小学生而言难度有点大！ 友友们，怎么看？有啥想法或思路，欢迎留言分享！ #小学数学#
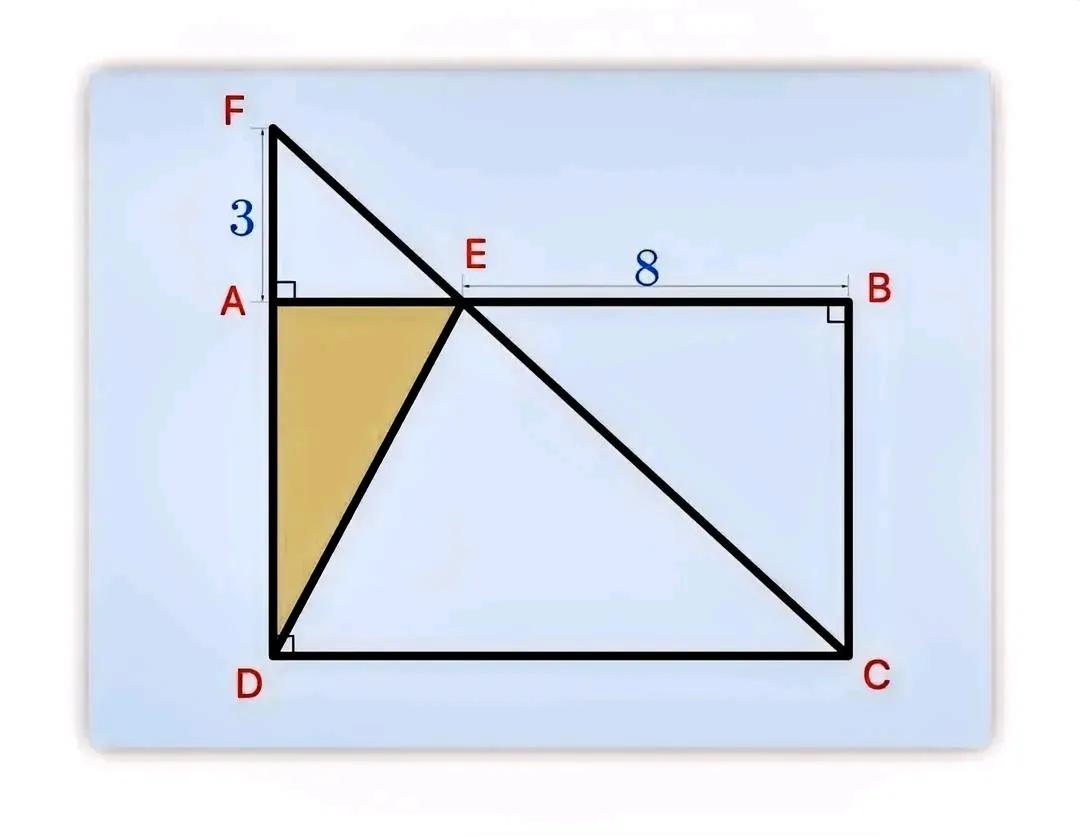
“貌似简单，会的寥寥无几！”这是一道小学五年级数学题：三角形仅一边已知，咋求面积
贝笑爱数学
2024-07-09 15:02:37
0
阅读：702
沉戈
3/AE=BC/8，AE*AD/2=AE*BC/2=12
杨百万在线
阴影面积=1/2 *3*8=12
司辰
反比例，这得初二，相似得出比，换成反比例得出积
海风椰影
设长方形宽为a，长为b，那么因为△AEF~△BCE，得3/a=（b-8）/8，整理得ab-a8=24，那么△AED面积=24/2=12。
用户32xxx27
连接AC,S△FAC-S△AEF+S△ECB=1/2S长方形ABCD，可求出AE*AD=24，S△ADE=12
用户12xxx76
如图，设AE=a，BC为b，因为△AEF与△BCE为对角相等的直角三角形，根据相似三角形定义可得3/b=a/8，即ab=24，那么S△ADE=ab/2=12
老张
题目出得巧妙，难度适中
浅梦易醒
如果用小学方法来解，条件是有点少。
用户13xxx82
这样补齐方形，通过三角形是方形的一半可以得知两个长方形是相等的，所以△AED=3*8/2=12
夏洛克丨福尔摩斯
以EC为折线，向内对折△EBC，产生新的△EB'C，且点B'必定在DC边上！！（剩下的就不用我说了吧）
夏丨叶 回复 宁静致远 07-13 20:52
。。。。。。你自己去画个图就明白了。。。。
宁静致远 回复 07-13 20:42
你首先得证明△CBE是个等腰三角形，或角BCE=角BEC。