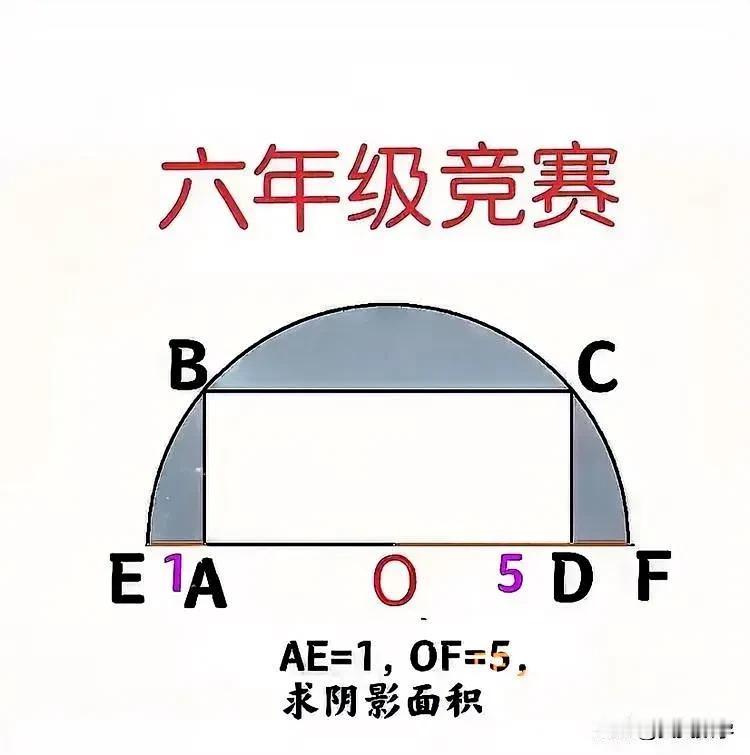
“难度太大，全军覆没！”不少家长认为，遗漏了条件（比如长方形的长宽比），否则仅用小学知识无法求解，非使用相交弦定理、三角形相似或射影定理等初中知识不可！这是一道小学六年级数学竞赛题：仅长已知，宽未知，咋求长方形面积？ 如图，半圆OEF内一长方形，AE=1，OF=5，求阴影部分面积（保留π）。 此题难在：仅用小学知识无法求出长方形的宽AB？ —————— 提示一：相交弦定理，适合初中生！ ①补齐圆：将整个半圆沿EF向下翻折，翻折后的长方形记为AB'C'D，则BCC'B'为长方形，直径EF垂直平分B'B，且AB=AB'。 ②由AE=1及OF=5，可知OD=5-1=4，AD=4×2=8，AF=2×5-1=9。 ③由相交弦定理，AB×B'A=AE×AF=9，从而AB=3，B'B=6。 ④S阴影=(S圆-S长方形BCC'B')÷2=25π/2-24。 提示二：三角形相似或射影定理，适合初中生！ ①同于提示一，可得AF=9。 ②连接BE和BF，则BEF为直角三角形。 ③△ABE∽△AFB，故AE/AB=AB/AF，从而AE=3。 或 ③'由射影定理可知AB²=AE×AF=9，即AB=3。 提示三：仅用小学知识无法求解，除非附加条件“AB：BC=3：8”。 如此，仅用小学知识能可求出AB=3。 友友们，怎么看？欢迎留言分享！ 小学数学
评论列表