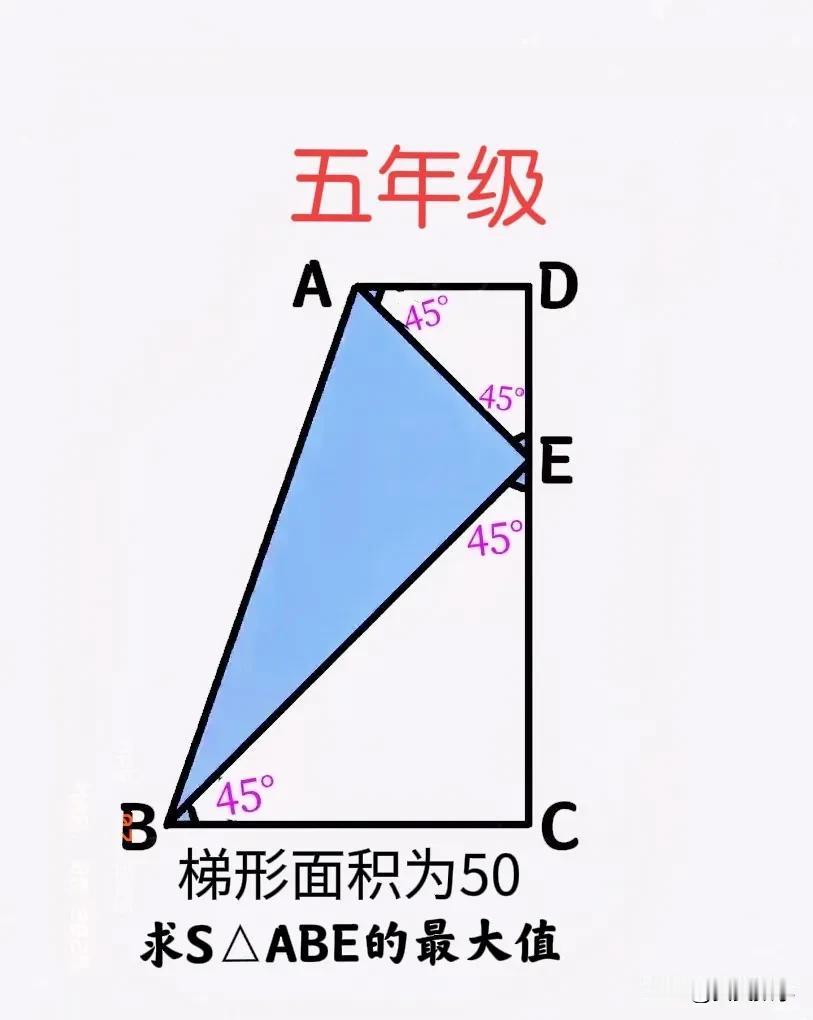
孩子们被这道题难哭了！老师说，全班没人做对，让大家回家再想想！小学五年级数学竞赛题：图形未定、边长未知，咋求直角三角形面积的最大值？ 如图，E为直角梯形ABCD腰CD上一点，连接AE和BE，将其分成一个直角三角形ABE和两个等腰直角三角形ADE与BCE，梯形面积为50，求三角形ABE面积的最大值。 —————————— 此题难在：梯形的形状不固定！只能求上下底之和为10，但无法求出上底、下底分别为多少） ——————————— 提示：先求梯形的高+化归！ ①AD=DE，BC=CE（即梯形的上下底之和与高相等），故S梯形ABCD=CD×CD÷2=50，从而CD=10。 ②化归：两个相同的梯形拼成1个边长为10的正方形，则2个阴影三角形拼成1个长方形（长为BE、宽为AE），据此问题可转化为求这个长方形面积的最大值或求两个等腰直角三角形面积和的最小值。 ③注意到长方形的周长是固定的，故当长宽相等（即AE=BE）时面积最大，从而DE=CE时，三角形ABE面积最大。此时DE=CE=5，两个等腰三角形面积相等，面积和为25，从而三角形ABE面积的为50-25=25，即其面积最大为25。 友友们，怎么看？欢迎留言分享！ 发优质内容享分成 分享数学思维题