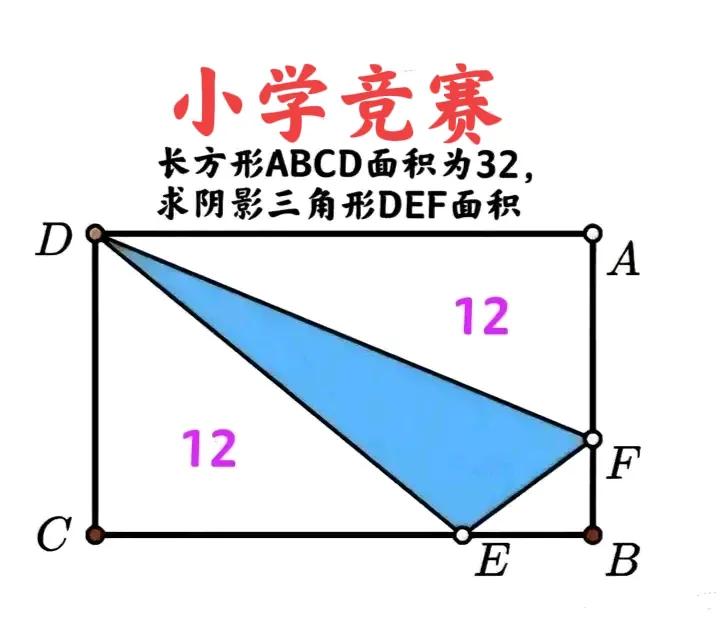
“几乎全军覆没,个别学霸除外!”有人说超纲了,有人说没超纲!这是一道小学数学竞赛题:三角形三边全都未知,求其面积! 如图,长方形ABCD的面积为32,三角形ADF与CDE的面积均为12,求阴影三角形DEF的面积。 有人说超纲了,非求解一元二次方程不可!过点E和F分别作AD和CD的垂线EG和FH,相交于点O。S△BEF记为a,则S△EOF=S△BEF=a,S△FOG=S△EOH=4-a,S△GOH=8+a。S△GOH/S△FOG=GO/OE=S△EOH/S△EOF也即(4-a)×(4-a)=a×(8+a)。 有人说不超纲,连接CF和AE即可!S△BCF=S△ABE=16-12=4,从而BC=4BE,AB=4BF,故S长方形ABCD=32S△BEF也即S△BEF=1。 友友们,怎么看?有啥想法或思路,欢迎留言分享! #小学数学#

体育老师
连接DB,ADB面积16。ADF面积12得出BF/AB为1/4,同理BE/BC也为1/4,三角形BEF面积为1,阴影面积为32-12-12-1=7
海风椰影
7
clay
连接BD即可,BD平分DEF+BEF,等高情况下,计算出BE:CE=1:3,BF:AF=1:3,设a为矩形底边b为矩形高,即BEF面积为1/2*(1/4)a*(1/4)b=(1/32)ab=1,DEF面积为32—12—12—1=7
杨百万在线
一眼看不出
嗄呗
连接DE,学完比例应该就会做这个题了, BF/CD=1/4,BE/CE=1/3,(等高的情况下,底边的比等于面积的比)。
浅梦易醒 回复 09-20 17:39
对的,比较或者分母都可以。得出长方形长8宽4就简单了。
用户16xxx72
连接BD,由等高三角形求得BE是BC的1/4和BF是AB的1/4,S三角形BEF=ABⅹBCⅹ1/4ⅹ1/4÷2=32ⅹ1/32=1,阴影面积=32-12ⅹ2-1=7
墨耘
比较好做,连接对角线,能看出同高底边比等于面积比,右下小三角形两条直角边为长方形两边的1/4,从而求出小三角形面积为1。阴影为7
不知不知
7。因为三角形EFB=1
无欲则刚
7