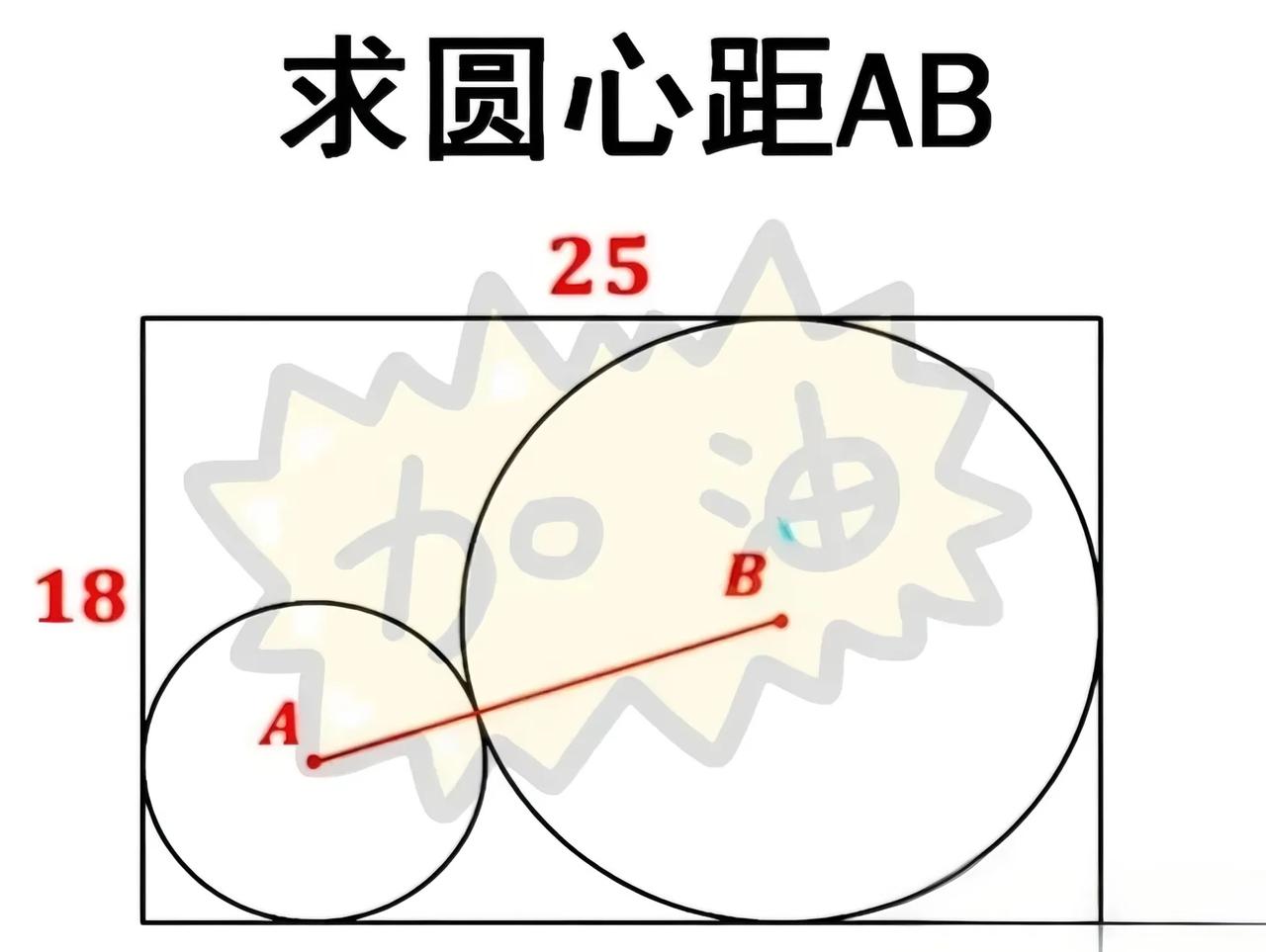
中考考场上，一道求圆心距AB的题难住众人。最后5分钟，学霸突然倒转试卷，全场目光聚焦。 大家都执着于用常规方法算圆心距离，学霸却发现暗藏玄机：矩形的18和25，结合两圆与矩形的位置关系，能构建特殊图形。巧用圆心角，把看似复杂的距离问题，转化为几何图形中线段关系 。当她快速写出答案，全场惊叹，掌声炸裂！这提醒我们，解题别被常规思路束缚，换个视角（像倒转试卷找新关联），结合图形隐藏条件，就能找到破局密码，数学的奇妙就在这些灵活转换里呀～
中考考场上，一道求圆心距AB的题难住众人。最后5分钟，学霸突然倒转试卷，全场目光
大力小学数学吖
2025-08-09 18:16:24
0
阅读：973
张力钧
已知大圆半径R＝9，设小圆半径为r，根据勾股定理： (9-r)²+(25-9-r)²＝(9+r)² 展开后解得r₁＝4，r₂＝-64（舍去） 圆心距＝R+r＝9+4＝13
用户15xxx26 回复 08-13 09:52
另外一个根是64哦，当然也是不符题意的
誓言
先这样做，在那样做，在这样做，就OK了
用户10xxx13
答案是4+9=13
用户15xxx89
设所求数为x，由题意可知x<18。过圆心分别作矩形边的平行线，得到以x为斜边的直角三角形，即有x^2=(25-x)^2 + (18-x)^2，展开得x^2 - 86x +949=0，即(x-13)(x-73)=0，已知x<18，故解得唯一解x=13。