[LG]《Reinforced Generation of Combinatorial Structures: Applications to Complexity Theory》A Nagda, P Raghavan, A Thakurta [UC Berkeley & Google & Google DeepMind] (2025)
利用AlphaEvolve助力复杂性理论的重大突破,推动组合结构发现新边界。
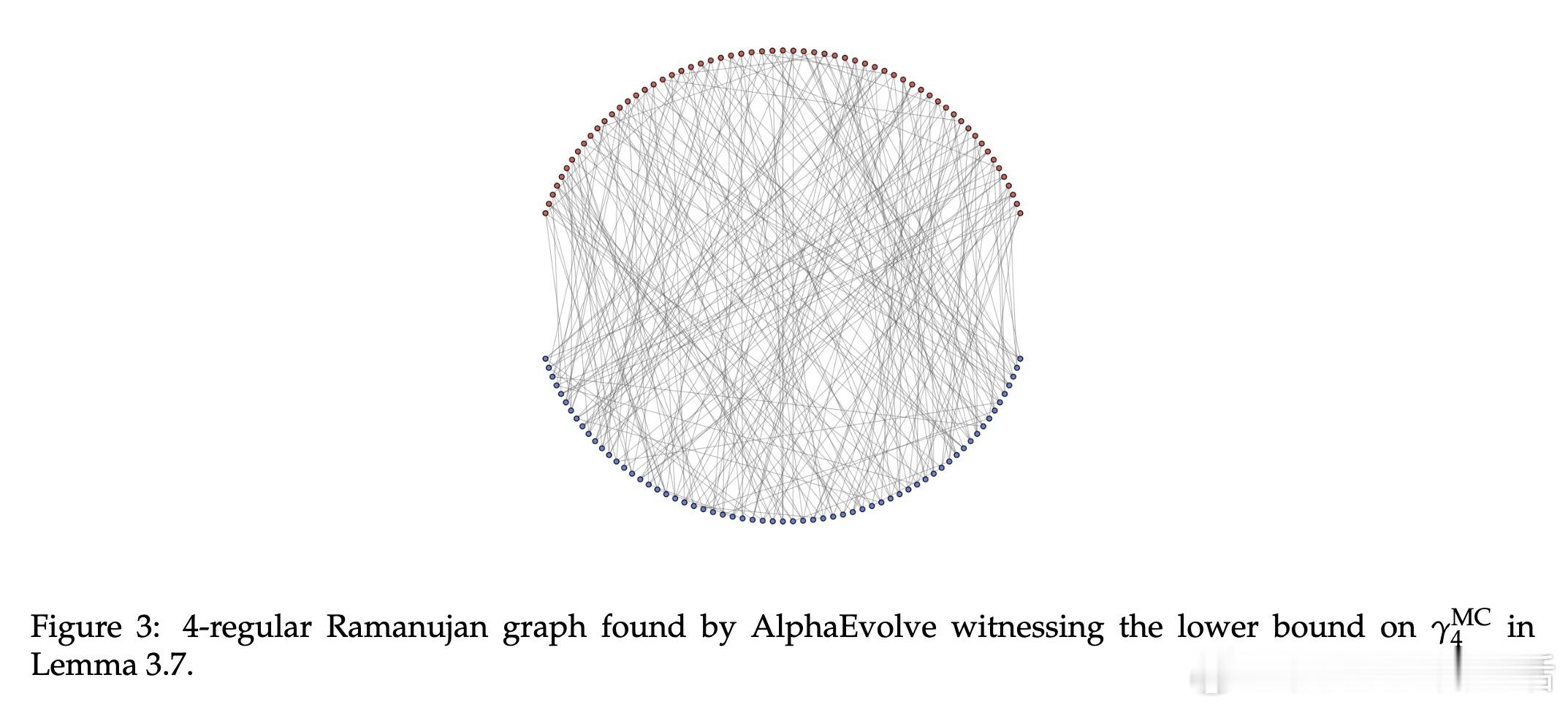
• 针对随机稀疏图的MAX-CUT与最大独立集问题,构建规模达163节点的极限Ramanujan图,显著提升了近似认证的下界,误差仅0.005,基本解决了小度数(3与4)情形的计算复杂度难题。
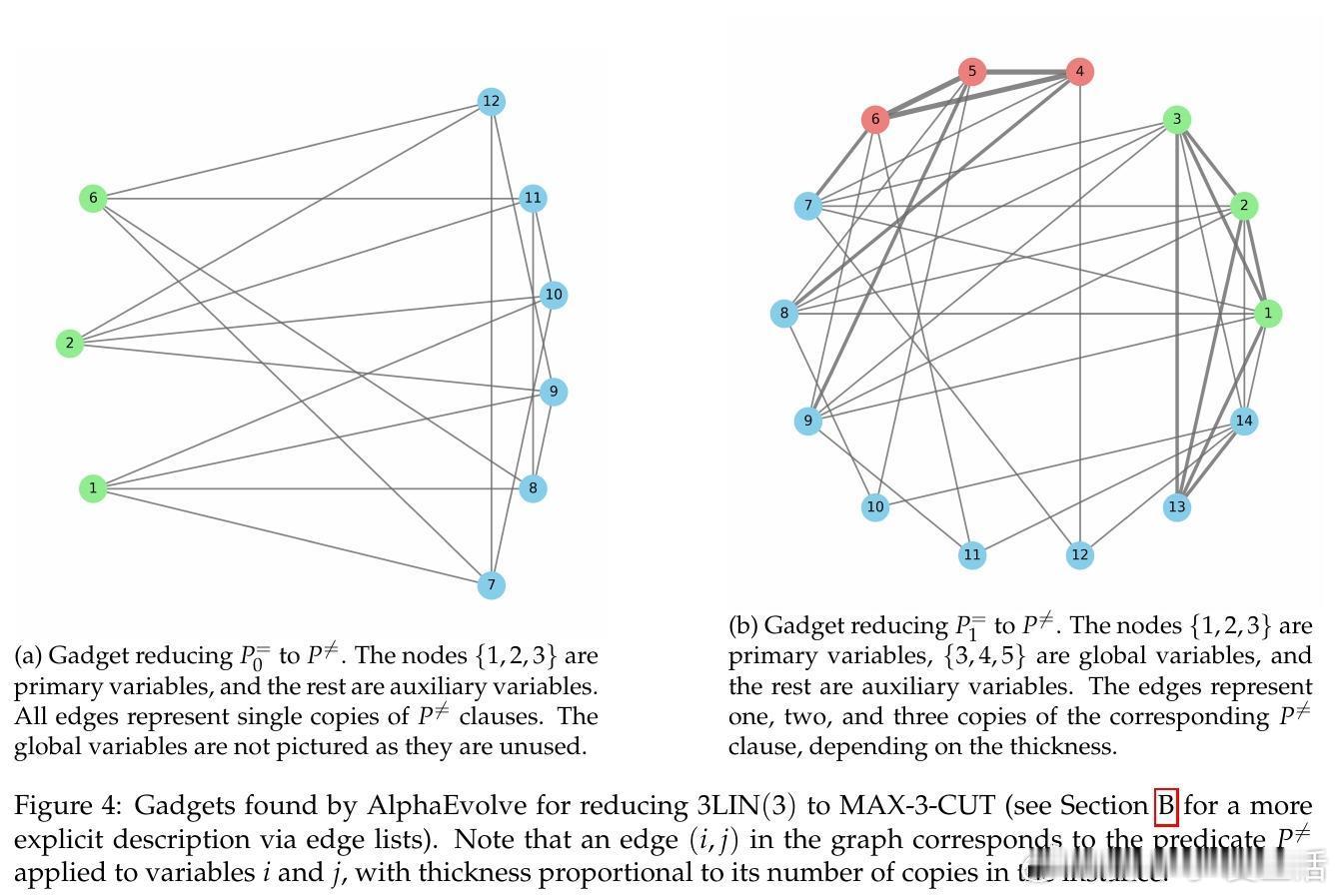
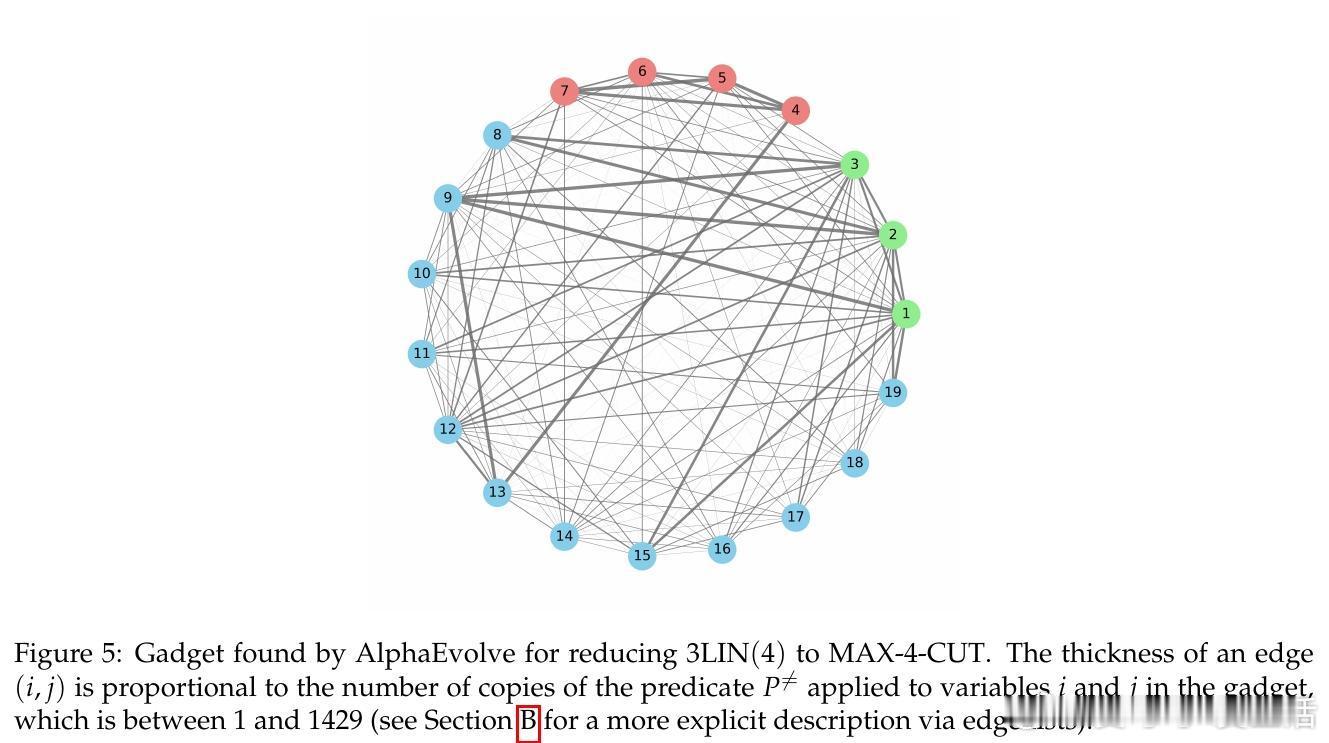
• 利用AlphaEvolve自主进化验证器,实现对NP-困难近似问题MAX-3-CUT和MAX-4-CUT的新难近似比0.9649与0.987,分别优于当前最佳小边界基于gadget的结果,且不依赖复杂PCP工具。
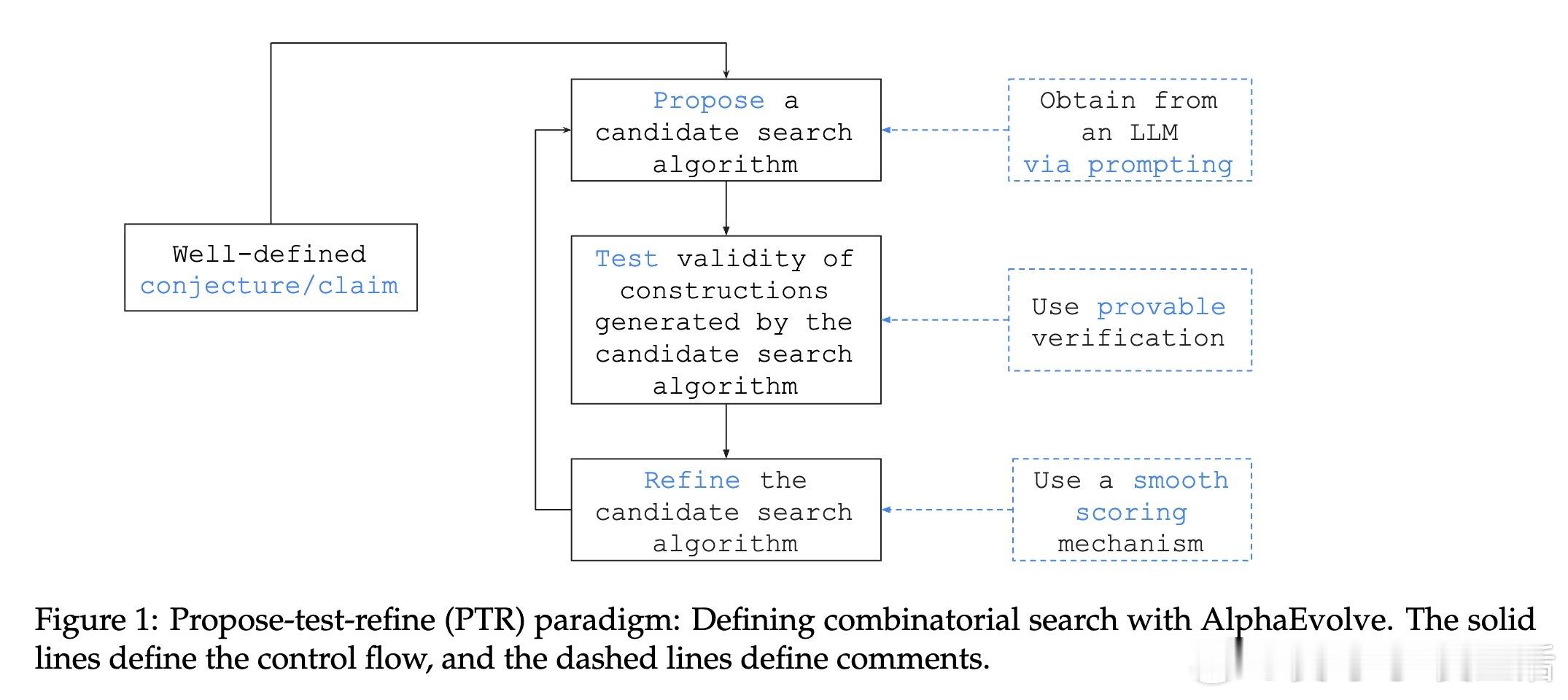
• 创新提出Propose-Test-Refine(PTR)范式,结合代码片段进化与平滑评分函数,强化组合结构搜索效率,尤其通过AlphaEvolve加速暴力验证达10,000倍,突破传统LP与MIP方法的规模瓶颈。
• 采用对称三元组结构和全局变量打破对称性,设计高效gadget,支持复杂映射关系,展示AI在数学构造中展现“代理推理”能力。
• 详尽的数学证明与代码实现确保结果可验证性与正确性,强调AI辅助发现的耐久性与可复现性,为未来AI与数学交叉研究树立范例。
心得:
1. AI不仅能总结前沿文献,还能在复杂组合空间中自主生成并验证极限结构,突破人工探索极限。
2. 高效验证器的加速是扩大搜索空间和构造规模的关键,体现了代码进化与系统优化的协同效应。
3. AI辅助数学研究强调“证据驱动”的可靠性,结合人类经验与自动验证,构成新型科研范式。
了解详情🔗arxiv.org/abs/2509.18057
人工智能复杂性理论组合优化算法数学自动化机器学习