[LG]《The Potential of Second-Order Optimization for LLMs: A Study with Full Gauss-Newton》N Abreu, N Vyas, S Kakade, D Morwani [Harvard University] (2025)
基于完整高斯-牛顿方法的二阶优化在大型语言模型中的潜力研究
随着LLM预训练计算需求激增,优化方法成为提升效率的关键。传统一阶优化如Adam固然流行,但二阶优化理论上收敛更快,尤其在大批量训练时优势明显。本文首次实测了全Gauss-Newton (GN) 预conditioning对高达1.5亿参数Transformer模型的影响,揭示了二阶优化的潜在极限。
🔑核心发现:
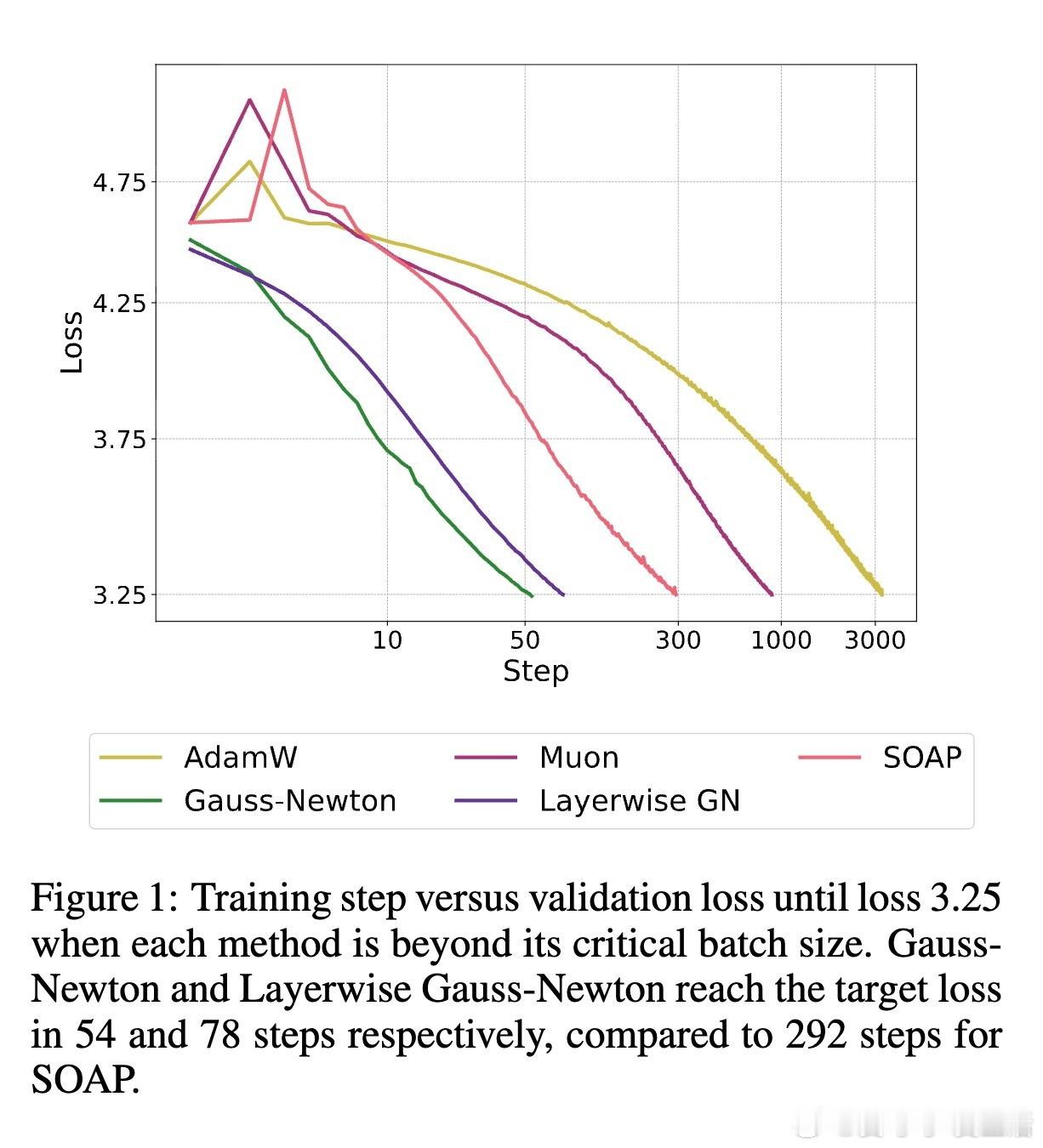
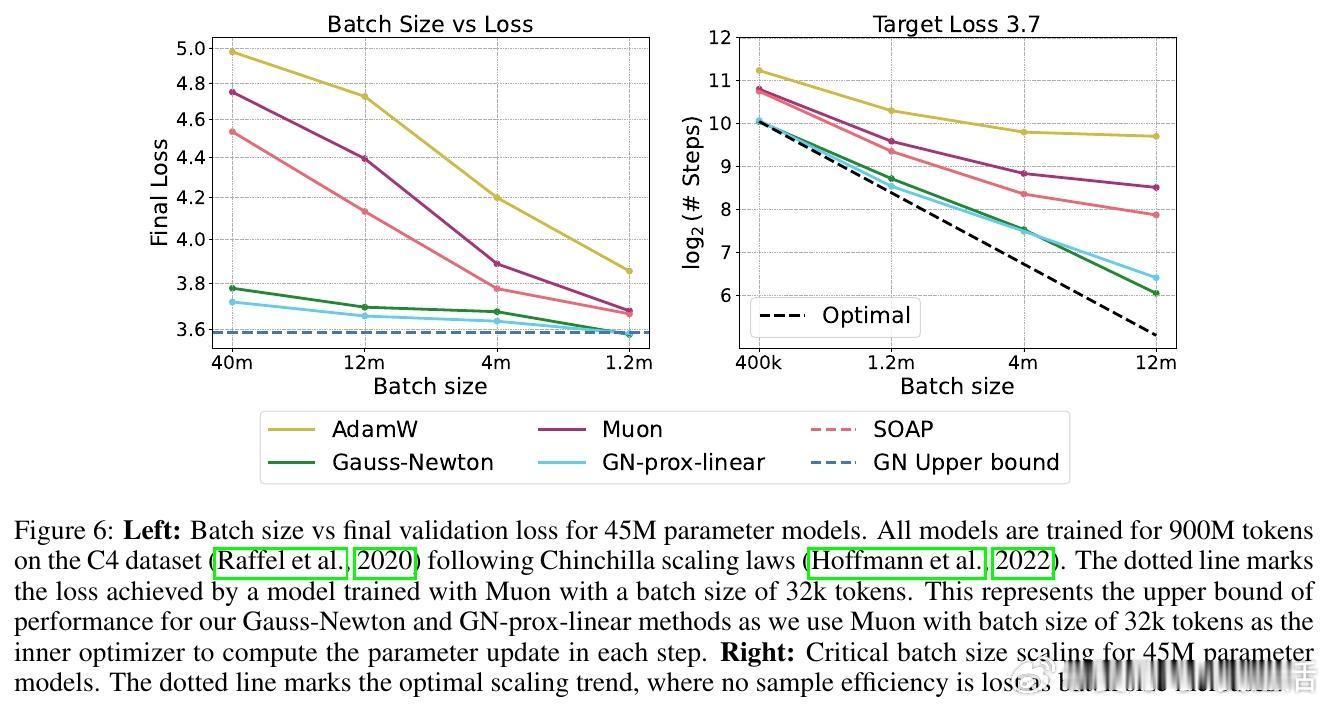
1️⃣ 全GN更新相比现有强基线(SOAP、Muon)迭代次数减少5.4倍,显著加速收敛。
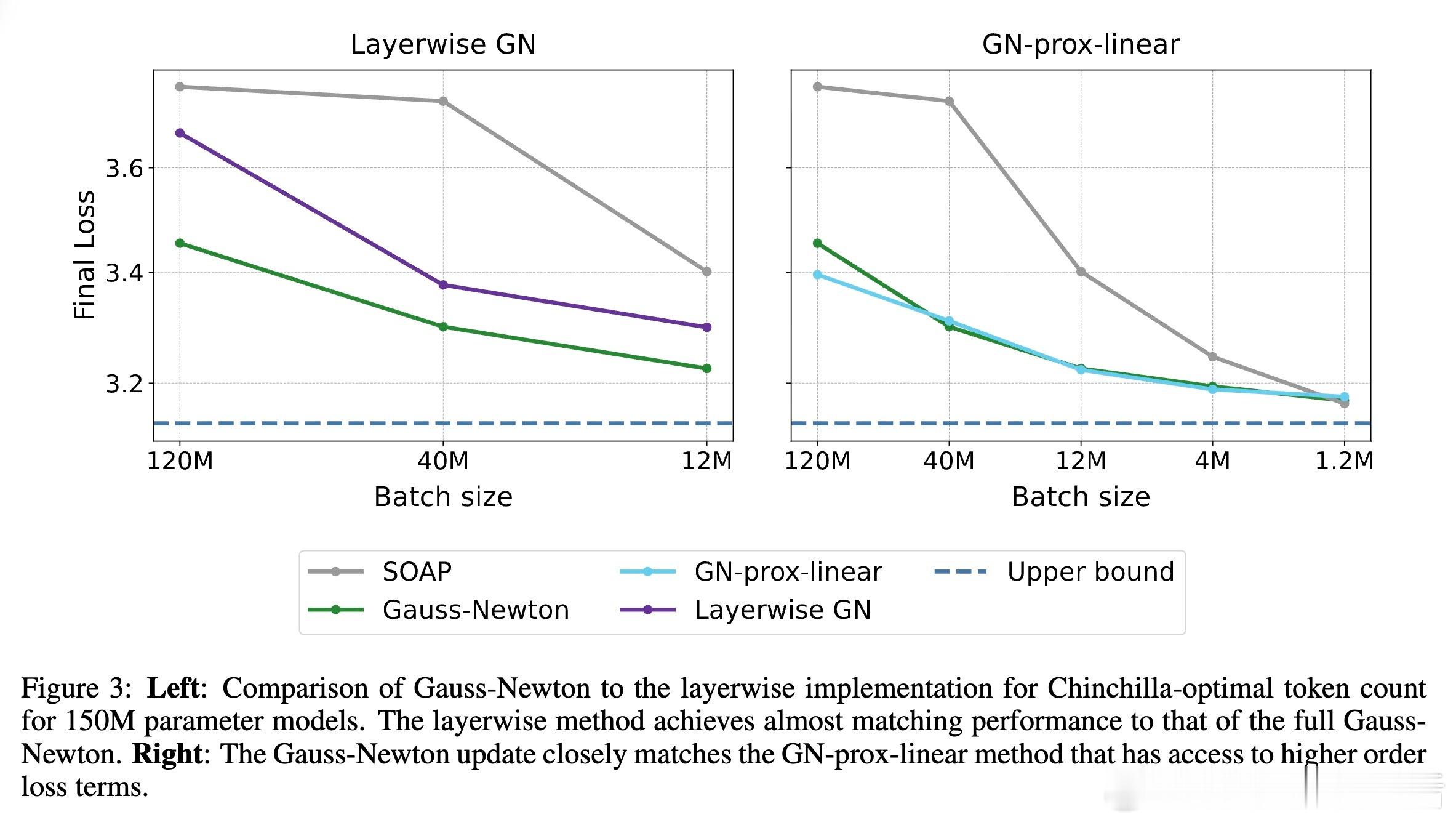
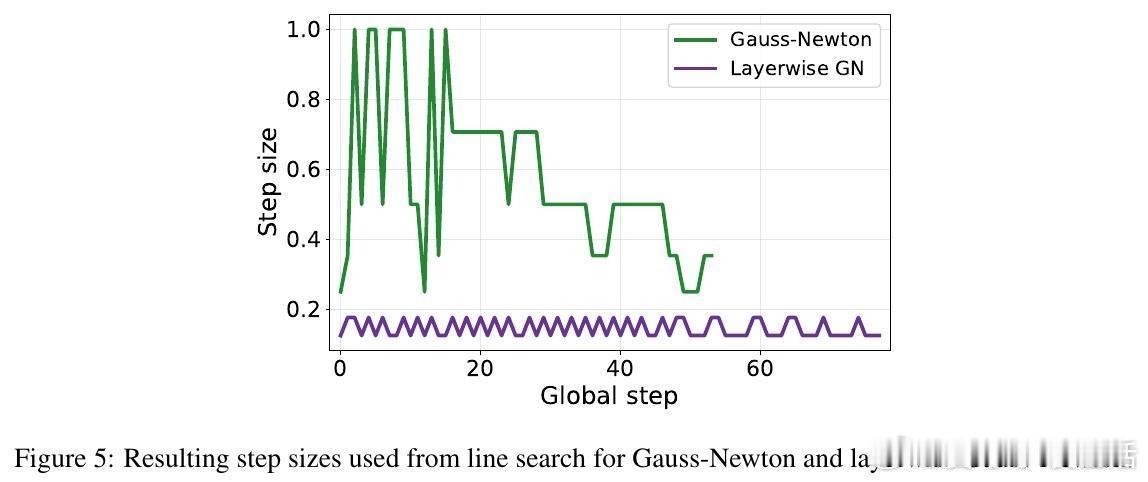
2️⃣ 精准的层级GN预conditioner(忽略跨层信息)性能几乎与全GN持平,说明层内Hessian结构已包含大部分关键信息。
3️⃣ 当前近似方法与理想层级oracle之间仍存在明显差距,暗示未来优化空间巨大。
📊实验亮点:
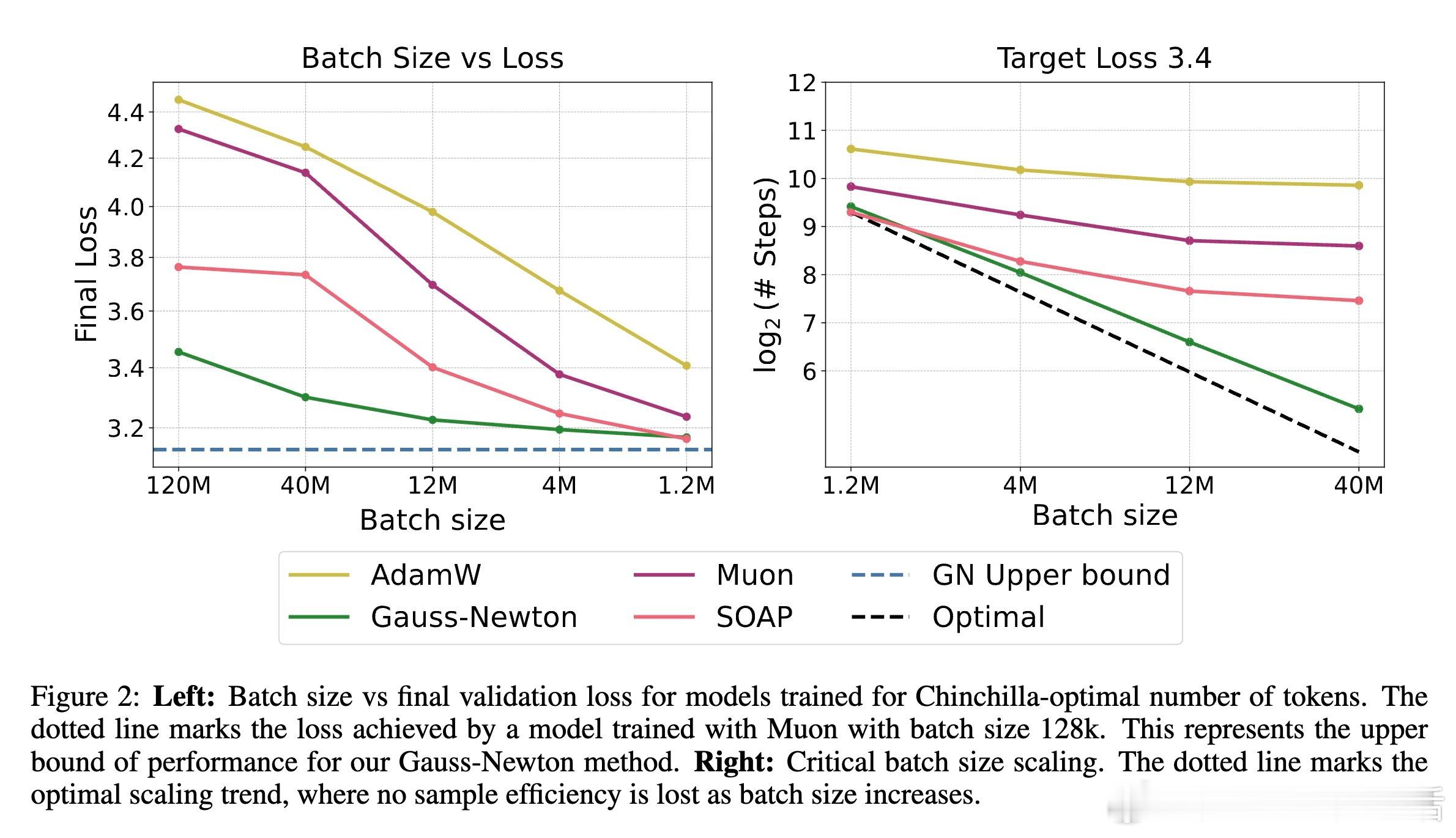
- 在超大批量(高于临界批量)下,全GN方法仍保持优秀的样本效率和迭代效率。
- GN-prox-linear方法(利用高阶损失信息)与全GN表现相近,表明高阶损失项对加速收敛影响有限。
- 层级GN方法在保持计算可行的同时,达到了接近全GN的方法性能,具备实际应用潜力。
⚙️方法细节:
- 通过Jacobian-向量积避免显式构造Hessian,实现了GN矩阵的可计算性。
- 采用Muon作为内层优化器解决二阶泰勒展开的最小化问题。
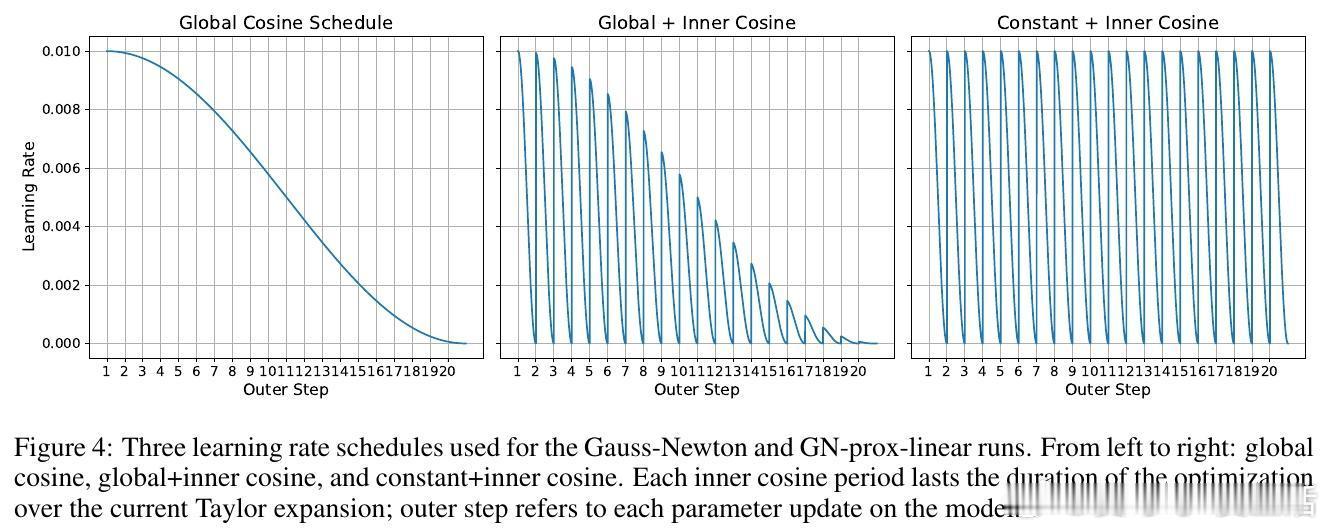
- 通过大规模超参数搜索和多种学习率调度确保稳定训练。
📝意义与展望:
- 本研究为二阶优化设定了性能上限,推动后续设计更高效、实用的二阶近似优化器。
- 层级GN的成功提示,未来可聚焦层内Hessian的高效表示与利用。
- 尽管目前全GN计算开销较大(训练速度约慢4-5倍),但证实其在大规模模型训练中的巨大潜力。
全文详见👉 arxiv.org/abs/2510.09378
机器学习 大语言模型 二阶优化 GaussNewton 深度学习优化 LLM训练 AI研究