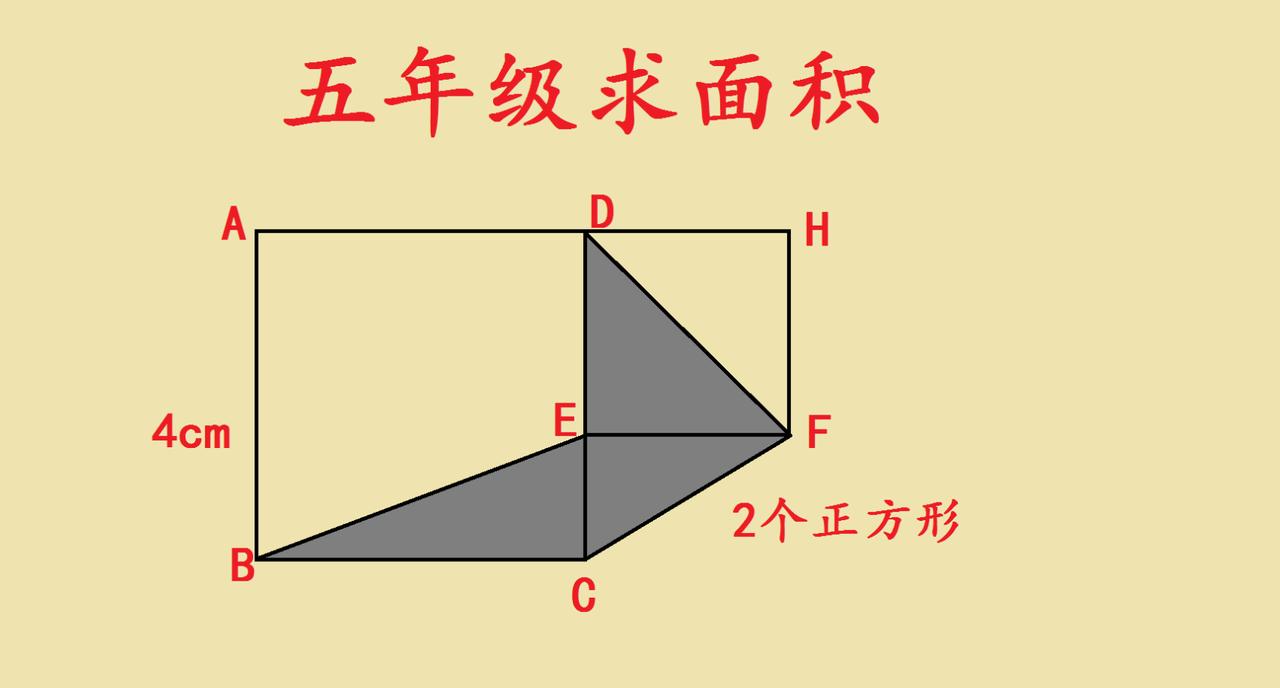
五年级的几何面积题里，藏着特别有趣的思维小机关～这道由两个正方形搭出的阴影面积题，乍一看图形分割得零散，好像要算好几块再相加，其实换个角度就能发现捷径。 试着观察阴影部分的形状，有没有发现它们的底和高，其实和正方形的边长藏着巧妙的对应关系？不用急着拆分计算，不妨试试“等积变形”的思路，把分散的阴影块通过平移、拼接，转化成我们熟悉的简单图形。 正方形的边长是解题的关键线索，当你找到阴影部分和正方形之间的面积关联，就会发现复杂的组合图形，其实能变成一个一眼就能看出答案的基础图形。几何题的乐趣就在于此，不是死算数值，而是用观察力和转化思维，把难题变简单。你找到这个隐藏的“图形密码”了吗？
评论列表
猜你喜欢
【4点赞】
【1评论】【7点赞】
【1评论】【1点赞】
作者最新文章
热门分类
看瓜切菜
把梯形HFDC旋转90度，放入大正方形里面，可以直观看出阴影面积正好是大正方形一半
金之鑫
已知正方形边长相等，所以DC＝BC、EF＝DE,因此DC×EF＝BC×DE,由此可证明⊿DFC与⊿BED面积相等，即阴影部分⊿DFC+⊿BEC＝⊿BED+⊿BEC＝⊿BDC, 也就是相当于正方形面积的一半。